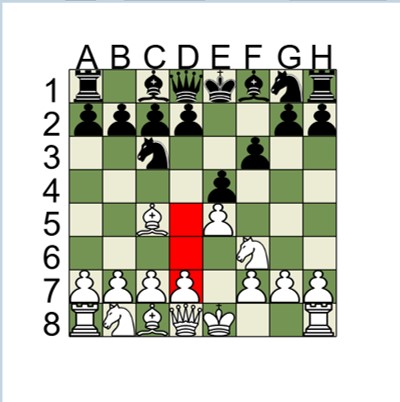
The program enables two persons to play a game of chess using the exercise model. Each player selects a piece and its destination for a move. The exercise displays allowable moves for each piece through showing red squares on the board. There are numerous design techniques used in the instruction set. These include state management arrays, extensive use of functions and codification of the board and associated GUI presentation. The game is not complete and enables the student to add features such as identifying a checkmate position, the castle move and en passant rules. Additional enhancement may include a player score and the display of taken pieces.

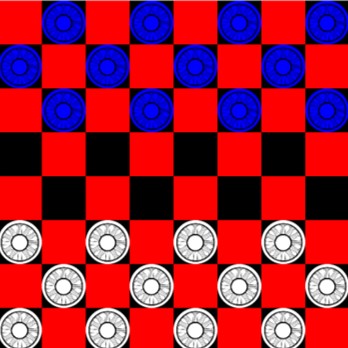
This exercise allows two players to square off in a checkers game. The game ensures only allowable moves can be made. The games does support pieces becoming a king and having the ability to move in any direction. This exercise is an excellent beginning set of instructions for students learning state management and rendering of codified GUI information. The “board” two dimensional array is used to maintain the location and status of each piece. Possible enhancements to the program includes displaying allowable moves, forcing piece capture and or maintaining a player score.

This video game demonstrates how the Breakout (or Brick Breaker) game can be modeled. The game employs an animation cycle to keep the shot from the base moving towards (and colliding) with the bricks. Various functions are used to identify collisions and render the new status of the screen. Boundary checks are provided to allow the shot to bounce off the top of the screen and continue to knock out the remaining bricks. Further enhancements could include additional key presses to affect the size and capability of the base, or to make the bricks move constants horizontally.

The race car exercise shows a race of up to 4 cars in a figure 8 racetrack. The user can click on a car and find out information about position and speed. A key challenge of this exercise is the use geometric functions that work with radians. The track is the shape of arcs which require distances to be measured with radians versus linear coordinates. A set of functions is used to perform the various tasks of updating the position of the car and rendering the car on the screen. Possible improvements would include enabling the user to have some form of control of a car, increasing the race length, and listing each car’s position and status during the race.

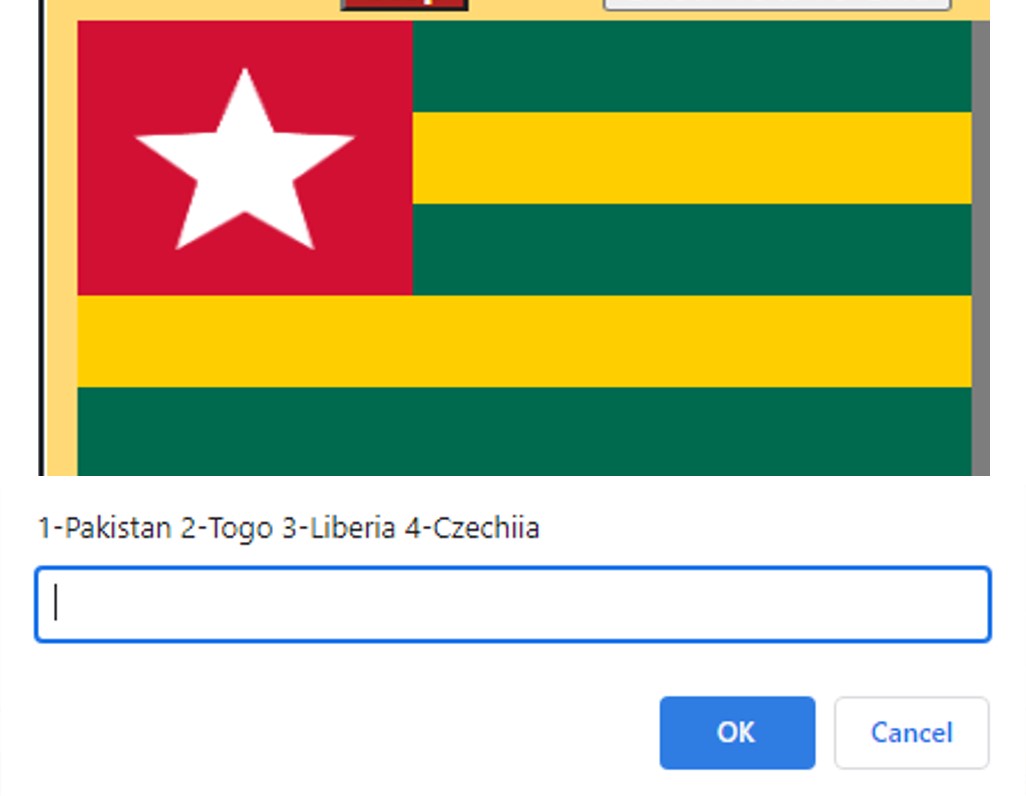
This exercise provides an opportunity for the student to see the generation of various flags from countries around the world. Each country’s flag generation is a separate function. The game itself is rudimentary with some randomness in selecting the answer. The choices shown with the correct answer are hard-coded, enabling an excellent assignment to enhance the game to uniquely generate alternative choices. Other enhancements would include display of the score while the game is in progress, and an input to end the game prematurely.

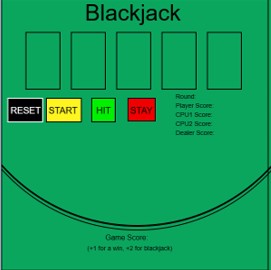
This exercise provides the framework for a blackjack with you as a player, two CPU players and the dealer. The cards are dealt and presented on the table. You, as a player, can receive another card (Hit) or keep your position (STAY). The exercise makes the decision for the other players. The exercise provides this logic and is ready for more advanced player decisions, and the implementation of rules such as 5 cards under 21 is a winning hand. Another exciting opportunity would be to have the system play all hands for thousands of games, where each automated player has a slightly different strategy. The best strategy could then be determined in this machine-learning style of analysis.

The Bingo exercise plays this traditional game automatically over 3 player boards. Numbers are chosen and player boards are dynamically updated. The card information is kept in a three dimensional array. The main function has a very clear set of function call that will manage the game. Enhancements to the game include duplicate numbers not being called during Bingo, although the generation of cards includes checking for duplicates. Enhancements would include modifying colors and cosmetic, adding more boards to a game, and changing the terms of winning to be the entire card.

This game is based solely on keypress inputs from the arrow keys. The player uses arrow keys to combine blocks of the same number into a higher power of 2. Each arrow stroke also introduces a new number (generally 2 or 4) onto the board. The game is played until one square has the number 2048 or no adjacent squares have the same number. State management is supported by an underlying two-dimensional array. A challenging enhancement would be for the computer to select the arrow keys and see the progress that can be made to reaching 2048 with random moves. The exercise demonstrates how games can be designed to be totally dependent on the event handlers.

This exercise provides the basic framework for a SuDoKu board. The board is randomly populated with numbers from 1 to 9, while respecting unique numbers in the row and columns (inner square not implemented). The user can enter a number to play and click on the desired location of the number. A state management two-dimensional array is employed and functions are provided to do duplicate checking and other move validations. The current exercise can be enhanced to provide more edits of the input, a score (number of squares left to populate), and possibly hints. A robust challenge is to have the computer randomly place numbers in squares until the SuDoKu solution is found. The main barrier to reaching a solution is that the current board is stuck on a configuration and can not move forward. At this point, backtracking (undoing previous square assignments) would need to be done to move along a different path to a possible solution.